给定一个长度为n的正整数数组A，其中所有数从左至右排成一排。
你需要将A中的每个数染成红色或蓝色之一，然后按如下方式计算最终得分：
设C为长度为n的整数数组，对于A中的每个数Ai（1≤i≤n）：
•如果Ai左侧没有与其同色的数，则令Ci=0。
•否则，记其左侧与其最靠近的同色数为Aj，若Ai=Aj，则令Ci=Ai，否则令Ci=0。
你的最终得分为C中所有整数的和，即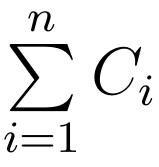
。你需要最大化最终得分，请求出最终得分的最大值。
从文件color.in中读入数据。
本题有多组测试数据。
输入的第一行包含一个正整数T，表示数据组数。
接下来包含T组数据，每组数据的格式如下：
第一行包含一个正整数n，表示数组长度。
第二行包含n个正整数A1,A2,...,An，表示数组A中的元素。
输出到文件color.out中。
对于每组数据：输出一行包含一个非负整数，表示最终得分的最大可能值。
3
3
1 2 1
4
1 2 3 4
8
3 5 2 5 1 2 1 4
1
0
8
【样例1解释】
对于第一组数据，以下为三种可能的染色方案：
1.将A1,A2染成红色，将A3染成蓝色（
），其得分计算方式如下：
•对于A1，由于其左侧没有红色的数，所以C1=0。
•对于A2，其左侧与其最靠近的红色数为A1。由于A1≠A2，所以C2=0。
•对于A3，由于其左侧没有蓝色的数，所以C3=0。
该方案最终得分为C1+C2+C3=0。
2.将A1,A2,A3全部染成红色（
），其得分计算方式如下：
•对于A1，由于其左侧没有红色的数，所以C1=0。
•对于A2，其左侧与其最靠近的红色数为A1。由于A1≠A2，所以C2=0。
•对于A3，其左侧与其最靠近的红色数为A2。由于A2≠A3，所以C3=0。
该方案最终得分为C1+C2+C3=0。
3.将A1,A3染成红色，将A2染成蓝色（
），其得分计算方式如下：
•对于A1，由于其左侧没有红色的数，所以C1=0。
•对于A2，由于其左侧没有蓝色的数，所以C2=0。
•对于A3，其左侧与其最靠近的红色数为A1。由于A1=A3，所以C3=A3=1。
该方案最终得分为C1+C2+C3=1。
可以证明，没有染色方案使得最终得分大于1。
对于第二组数据，可以证明，任何染色方案的最终得分都是0。
对于第三组数据，一种最优的染色方案为将A1,A2,A4,A5,A7染为红色，将A3,A6,A8染为蓝色（
），其对应C=[0,0,0,5,0,1,2,0]，最终得分为8。
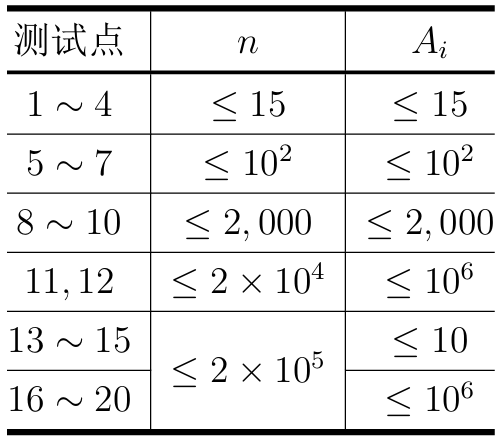
【数据范围】
对于所有测试数据，保证：1≤T≤10，2≤n≤2×10^5，1≤Ai≤10^6。
