为了写作业,小可可和小多在下一种奇怪的棋——hex 棋。
如下是一个这种棋的棋盘,它可能可以帮助你理解下面的题意:
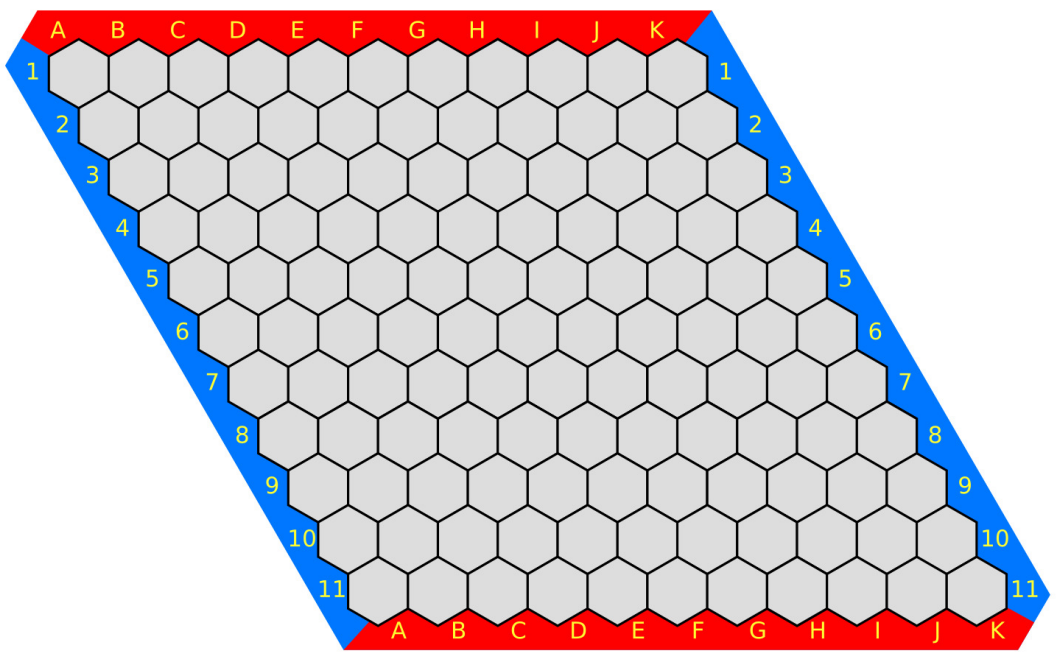
这种棋的规则如下:
棋盘由 N × N 个六边形格子构成。
称两个格子相连通,当且仅当两个格子对应的六边形共边。
将从上往下第 i 行从左到右第 j 个格子称为 (i, j)。对于一个不在边界上的格子 (i, j),它和 (i, j + 1),(i, j − 1),(i + 1, j),(i + 1, j − 1),(i − 1, j),(i − 1, j + 1) 这些格子相连通,而边界上的格子只与上述格子中存在的格子相连通。
两人轮流下棋,小可可先手,小可可每次选一个空的格子下一个红色棋子,小多每次选一个空的格子下一个蓝色棋子,如果小可可将上下两条边界用红色棋子连通了,那么小可可胜;如果小多将左右两条边界用蓝色棋子连通了,那么小多胜。
接下来给出若干个局面,请你判断每一局是小可可胜,还是小多胜,还是目前没有人获得胜利(容易证明,不可能两人都达到获胜条件)。
输入文件名为 hex.in。
第一行一个正整数 T,代表他们下了 T 盘棋。
对于每一盘棋:
输入一行一个正整数 N,代表目前这盘棋的棋盘的大小。
之后 N 行,每行 N 个 −1, 0, 1 中的整数,第 i 行的第 j 个整数代表格子 (i, j) 的状态,如果为 −1 则该格子中为蓝色棋子,如果为 0 则该格子为空,如果为 1 则该格子中为红色棋子。
输出文件名为 hex.out。
输出共 T 行,请对于每个局面,输出一行一个字符串:如果小可可胜,则输出 ke;如果小多胜,则输出 do;如果目前两人都还未获胜,则输出 yet。
3
4
0 1 0 -1
0 -1 1 0
-1 -1 1 0
0 0 1 0
4
0 1 1 -1
0 -1 1 0
-1 -1 1 0
0 0 1 0
4
0 1 -1 -1
0 -1 1 1
-1 -1 1 0
0 0 1 0
yet
ke
do
【样例 1 解释】
在第一个棋盘中,不存在将上下边界连通的红色棋子序列,也不存在将左右边界连通的蓝色棋子序列,故目前未分出胜负。
在第二个棋盘中,上下两个边界由 (1, 3),(2, 3),(3, 3),(4, 3) 这些红色棋子连通了,所以小可可获胜了。
在第三个棋盘中,左右两个边界由 (3, 1),(2, 2),(1, 3),(1, 4) 这些蓝色棋子连通了,所以小多获胜了。
【数据规模与约定】
对于 20% 的数据,满足 1 ≤ N ≤ 3。
对于另外 40% 的数据,满足给出的棋局已经分出胜负。
对于 100% 的数据,满足 1 ≤ T ≤ 10,1 ≤ N ≤ 100。
更新记录:请不要直接输出样例,20241220 已更新测试数据